✒️ 论文公式总结

GIoU

$GIoU = IoU_{3d} - \frac{V_c - U}{V_c}$

其中，$V_c$代表能够包含两个框的最小立方体体积。$U$代表两个检测框的交集体积。

L2 distance

L2距离是简单的欧几里得距离。

$D_{\text{L2}}(\mathbf{x}, \mathbf{y}) = \sqrt{\sum_{i=1}^n (x_i - y_i)^2}$

Kalman Filter

Kalman滤波器是一种用于预测和估计动态系统的状态的滤波方法。下面是它在MOT中的常见形式。（CV/CA模型）

$$ \begin{align*} x_{\text{pre}} &= A \cdot x \\ P_{\text{pre}} &= A \cdot P \cdot A^T + Q \\ K_k &= P_{\text{pre}} \cdot H^T / (H \cdot P_{\text{pre}} \cdot H^T + R) \\ x &= x_{\text{pre}} + K_k \cdot (z - H \cdot x_{\text{pre}}) \\ P &= (I - K_k \cdot H) \cdot P_{\text{pre}} \end{align*} $$
注意，filterpy库中的实现是略有不同的。对于最后一个公式，它进行了一定的修正。

Extended Kalman Filter

扩展卡尔曼滤波器是基于普通卡尔曼滤波器的扩展，用于处理非线性系统。其原理是对模型进行泰勒一阶展开，从而处理非线性系统。下面是对常用非线性模型CTRV的扩展卡尔曼滤波器的数学公式。

$$ \begin{align*} x_{pre} &= \begin{bmatrix} x_{pre} \\ y_{pre} \\ v_{pre} \\ \theta_{pre} \\ \omega_{pre} \end{bmatrix} = x + \begin{bmatrix} \frac{v}{\omega} \left( \sin(\omega \cdot \text{dt} + \theta) - \sin(\theta) \right) \\ \frac{v}{\omega} \left( \cos(\theta) - \cos(\omega \cdot \text{dt} + \theta) \right) \\ 0 \\ \omega \cdot \text{dt} \\ 0 \end{bmatrix} \\ P_{\text{pre}} &= J \cdot P \cdot J^T + Q \\ K_k &= P_{\text{pre}} \cdot J_h^T / (J_h \cdot P_{\text{pre}} \cdot J_h^T + R) \\ x &= x_{\text{pre}} + K_k \cdot (z - h(x_{\text{pre}})) \\ P &= (I - K_k \cdot J_h) \cdot P_{\text{pre}} \end{align*} $$

HOTA: A Higher Order Metric for Evaluating Multi-object Tracking

HOTA可以被视为三个IoU得分的组合。它将跟踪评估任务分为三个子任务（检测、关联和定位），并使用IoU（交并比）公式（也称为杰卡德指数）为每个子任务计算得分。

  1. 定位： 用于衡量追踪框和真实框之间的重合程度
$$LocIOU = \frac{Intersection}{Union}$$$$LocA = \frac{1}{|TP|} \sum_{c \in TP} \mathrm{Loc-IoU}(c)$$
  1. 检测： 衡量所有预测检测集合与所有真实检测集合之间的对齐程度
$$\mathrm{DetA} = \frac{|TP|}{|TP| + |FN| + |FP|}$$
  1. 关联： 衡量预测关联集合与真实关联集合之间的对齐程度
$$\mathrm{AssA} = \frac{1}{|TP|} \sum_{c \in TP} \mathrm{Ass-IoU}(c) = \frac{1}{|TP|} \sum_{c \in TP} \frac{|TPA(c)|}{|TPA(c)| + |FNA(c)| + |FPA(c)|} $$

最后综合考虑上面的三个方面，得到HOTA指标。（可能注意到没有LocA，因为这个指标内化在确定DetA和AssA中）

$$\mathrm{HOTA}_{\alpha} = \sqrt{\mathrm{DetA}_{\alpha} \cdot \mathrm{AssA}_{\alpha}}$$

和其他指标的区别：

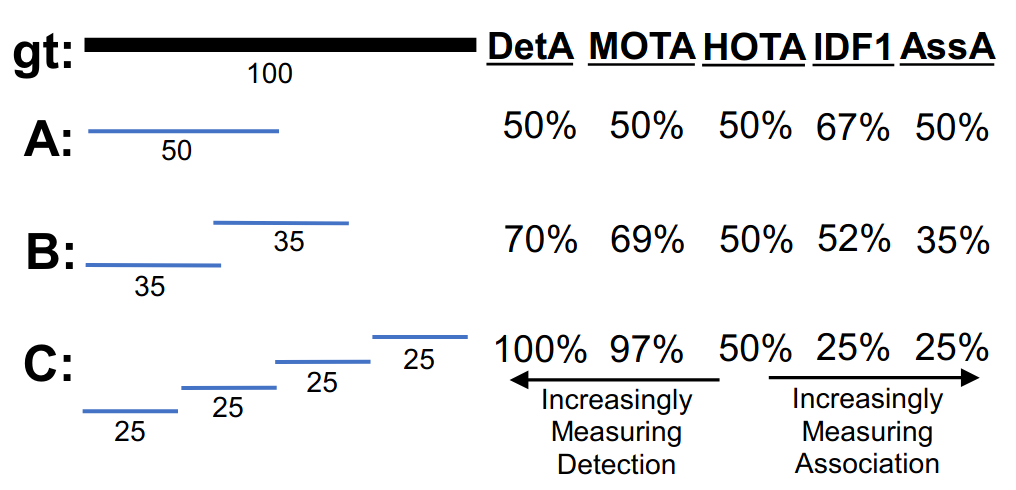
我们可以通过下面这个例子看到，在HOTA中关联和检测的权重几乎相同，而不是想MOTA中那样，检测的权重明显更高。我认为这是非常合理的。

指标之间的区别

KITTI坐标变换公式

mmdetection3d详细文档

$$ \mathbf{y} = \mathbf{P}_{rect}^{i} \cdot \mathbf{R}_{rect}^{0} \cdot \mathbf{T}_{velo}^{cam} \cdot \mathbf{x} $$

推导过程：

  1. 点云齐次坐标（激光雷达坐标系）
$$\mathbf{x} = \begin{bmatrix} x_{velo} \\ y_{velo} \\ z_{velo} \\ 1 \end{bmatrix} \quad (4 \times 1 \text{列向量})$$
  1. 激光雷达到相机的外参矩阵
$$\mathbf{T}_{velo}^{cam} = \begin{bmatrix} \mathbf{R}_{3 \times 3} & \mathbf{T} \\ \mathbf{0}_{1 \times 3} & 1 \end{bmatrix} \quad (4 \times 4 \text{矩阵})$$
  1. 相机坐标系矫正矩阵（畸变矫正）
$$\mathbf{R}_{rect}^{0} = \begin{bmatrix} \mathbf{R}_{rect\_00}^{3 \times 3} & \mathbf{0} \\ \mathbf{0}_{1 \times 3} & 1 \end{bmatrix} \quad (4 \times 4 \text{矩阵，由3×3矩阵扩展})$$

注意，该步骤得到4*1列向量(x,y,z,1)，当z小于0时，说明该点在相机后侧，应该被忽略。

  1. 相机内参矩阵（映射到i号相机图像）
$$\mathbf{P}_{rect}^{i} \quad (3 \times 4 \text{矩阵})$$
  1. 图像坐标（齐次形式）
$$\mathbf{y} = \begin{bmatrix} x_{cam} \\ y_{cam} \\ Z_c \end{bmatrix} \quad (3 \times 1 \text{列向量})$$
  1. 最终图像坐标（归一化后）
$$\text{图像坐标} = \left( \frac{x_{cam}}{Z_c}, \frac{y_{cam}}{Z_c} \right)$$
  1. 完整映射公式
$$\mathbf{y} = \mathbf{P}_{rect}^{i} \cdot \mathbf{R}_{rect}^{0} \cdot \mathbf{T}_{velo}^{cam} \cdot \mathbf{x}$$